About the Dihedral Angle Calculator

The Dihedral Angle Calculator is a powerful online tool for analyzing protein structures by calculating Phi (φ) and Psi (Ψ) dihedral angles for every residue in a given protein. Simply upload a .pdb file or enter a PDB ID to quickly compute these angles and generate a detailed Ramachandran Plot.

Designed for researchers, educators, and students in bioinformatics and structural biology, this tool offers an intuitive interface for exploring protein conformations. Results can be viewed in an interactive table or downloaded in popular formats like CSV, Excel, PDF, and TXT, making it easy to integrate with your research workflow. Enhance your understanding of protein folding, dihedral angles, and molecular interactions with this indispensable tool for protein structure analysis. Whether you're studying protein dynamics or conducting biochemical research, the Dihedral Angle Calculator provides precise and accessible insights for better scientific discovery.

How Would You Like to Begin?

How to Make the Most of This Tool

Choose your Input Method

Upload or Select .pdb files for processing.

Angle Calculation

Phi and Psi angles will be automatically calculated for all residues by the tool.

Ramachandran Plot

A Ramachandran Plot will also be generated.

Interactive Table

The results will be viewable in an interactive, scrollable table.

Download Options

The results will be available in CSV, Excel, PDF, and TXT formats.

Tips for Success

Ensure accurate PDB IDs and file size within 50 MB.

What is Dihedral Angles

A dihedral angle in a protein refers to the internal angle formed between two adjacent planes of the polypeptide backbone. The backbone connects amino acids through peptide bonds, forming a chain. The shape of this backbone, how it bends and twists, determines the overall structure and function of the protein.

The backbone between two neighboring Cα atoms lies in a single plane, and the conformation of the backbone can be described using two dihedral angles for each amino acid residue. These angles are called φ (phi) and ψ (psi):

  • φ (phi): Involves the atoms C-N-Cα-C, describing the rotation around the bond between the nitrogen and the Cα atom.
  • ψ (psi): Involves the atoms N-Cα-C-N, describing the rotation around the bond between the Cα atom and the carbonyl carbon.
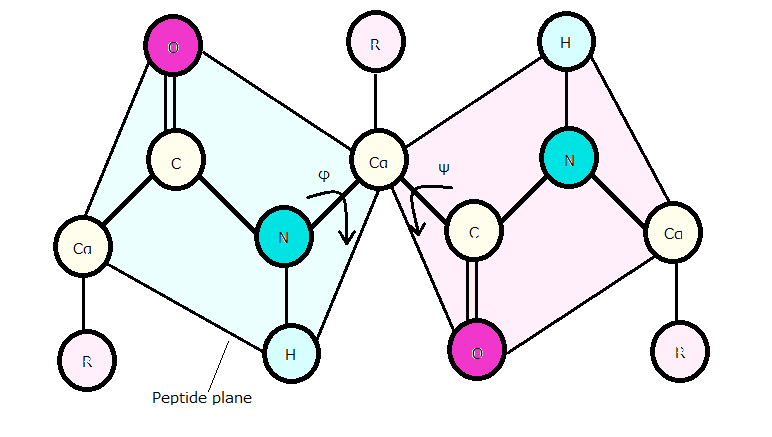
Diagram of dihedral angles φ (phi) and ψ (psi) in a protein structure
Dihedral angles φ (phi) and ψ (psi) in amino acid residues

The values of φ and ψ are restricted by steric hindrance, which happens when atoms interfere with each other’s space. Atoms such as the carbonyl oxygen, hydrogen of the NH group, and side-chain atoms limit the angles, ensuring the protein folds into a stable and functional shape.

The way a protein folds is influenced by these dihedral angles. Proteins must adopt specific shapes to perform their biological functions, such as catalyzing reactions or binding to other molecules. By studying φ and ψ angles, scientists can predict how proteins will fold and their functions.

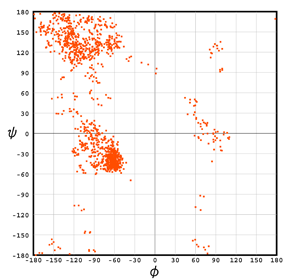
What Is a Ramachandran Plot?

A Ramachandran plot is a graphical tool used to visualize the relationship between φ and ψ angles in a protein. It helps researchers understand the allowed and forbidden regions of these angles, showing which combinations are physically possible in protein structures.

The plot has key regions corresponding to the two most common protein conformations:

  • Alpha helix (α helix): Found around the coordinates (-60, -50) in the plot. This structure forms a right-handed spiral.
  • Beta sheet (β sheet): Found around (-120, 120). The protein backbone forms flat, extended sheets.
  • Left-handed α helix: A rare structure, found around (60, 60) in the plot.

By analyzing a Ramachandran plot, researchers can verify if a protein’s conformation is stable and realistic, ensuring that proteins fold correctly to perform their functions.

Ramachandran Plot
Ramachandran Plot

Frequently Asked Questions

The tool calculates the phi (Φ) and psi (Ψ) dihedral angles for all residues in a protein structure, visualizes these angles in a Ramachandran plot, and provides downloadable results for further analysis. It is designed for researchers, educators, and students to analyze protein conformations efficiently.

The tool accepts either a 4-character PDB ID (e.g., 1ajq) or a .pdb file upload. Users can input a PDB ID to fetch the structure directly from online repositories or upload a local PDB file for analysis.

Φ (phi) is the rotation around the N-Cα bond (atoms involved: C-N-Cα-C), and Ψ (psi) is the rotation around the Cα-C bond (atoms involved: N-Cα-C-N). The angles are calculated using vector mathematics by determining the angles between planes formed by these atoms in the protein backbone.

The Ramachandran plot visualizes the φ and ψ dihedral angles, identifying allowed and disallowed regions. It validates protein models by ensuring residues fall within sterically allowed regions (e.g., α-helix, β-sheet).

The tool identifies missing residues and marks them as "Missing Residue" in the output. This ensures users are aware of incomplete data without disrupting the calculation process.

Key features include visualization through Ramachandran plots, interactive sortable tables, multiple download options (CSV, Excel, PDF, TXT), and error handling for invalid inputs.

Steric hindrance limits φ and ψ angles, creating allowed regions in the Ramachandran plot corresponding to secondary structures like α-helices (-60°, -50°) and β-sheets (-120°, 120°).

The tool parses PDB files or fetches data using PDB IDs, calculates φ and ψ angles using standard algorithms, and plots the angles on a Ramachandran plot for visualization.

Glycine is more flexible due to its lack of a side chain, while proline's cyclic structure restricts its φ and ψ angles, creating unique patterns on the plot.

Results can validate protein structure quality, model folding pathways, analyze flexibility, and provide input for molecular dynamics simulations or secondary structure predictions.
Author Photo

Om Prakash

A passionate bioinformatics enthusiast and developer, blending biology and technology to uncover new discoveries. Passion, patience, and understanding are qualities I’ve nurtured since childhood. Helping others and sharing knowledge are my daily practices.

Get in Touch

Got questions or feedback? We’re here to help! Fill out the form below, and we’ll get back to you as soon as possible.

Share the Dihedral Angle Calculator

Help others discover the Dihedral Angle Calculator by sharing it on your favorite platform!

Share on Facebook
Share on Twitter
Share on LinkedIn
Share on WhatsApp